Chapter 3: VARIABLES AND EXPRESSIONS
Variables are of 2 kinds:
|
1) file variables |
(read from disk files) |
|
2) user-defined variables |
(defined by the user with LET command) |
Both types may be accessed identically in all commands and expressions.
Variables, regardless of kind, possess the following associated information:
1)
grid—the underlying coordinate structure
2) units
3) title
4) title modifier
(additional explanation of variable)
5) flag value for missing data points
Use the commands SHOW DATA and SHOW VARIABLES to examine file variables and user-defined variables, respectively.
The pseudo-variables I, J, K, L, X, Y, Z, T and others may be used to refer to the underlying grid locations and characteristics and to create abstract variables.
Variables in Ferret are referred to by names with optional qualifying information appended in square brackets. See DEFINE VARIABLE (p. 262) for a discussion of legal variable names.
The information that may be included in the square brackets includes
D=data_set_name_or_number ! indicate the data set
G=grid_or_variable_name
! request a regridding
X=,Y=,Z=,T=,I=,J=,K=,L= ! specify
region and transformation
See the chapter "Grids and Regions", section "Regions" (p. 118) for more discussion of the syntax of region qualifiers and transformations.
Some examples of valid variable syntax are
Myvar ! data set and region as per current context
myvar[D=2]
! myvar from data set number 2 (see SHOW DATA, p. 320)
myvar[D=a_dset]
! myvar from data set a_dset.cdf or a_dset.des
myvar[D=myfile.txt] !
myvar from file myfile.txt
myvar[G=gridname] ! myvar regridded to grid
gridname
myvar[G=var2] ! myvar regridded to the grid of var2
! which is in the same data set as myvar
myvar[G=var2[D=2]]
! myvar regridded to the grid of var2
! which is in
data set number 2
myvar[GX=axisname] ! myvar regridded to a dynamic grid
which
! has X axis axisname
myvar[GX=var2] ! myvar
regridded to a dynamic grid which
! has the X axis
of variable var2
myvar[I=1:31:5] ! myvar subsampled at every 5th point
! (regridded to a subsampled axis)
myvar[X=20E:50E:5]
! myvar subsampled at every 5 degrees
! (regridded
to a 5-deg axis by linear interpolation)
File variables are stored in disk files. Input data files can be ASCII, binary, NetCDF, or TMAP-formatted (see the chapter "Data Set Basics", p. 29). File variables are made available with the SET DATA (alias USE) command.
In some netCDF files the variable names are not consistent with Ferret's rules for variable naming. They may be case-sensitive (for example, variables "v" and "V" defined in the same file), may be restricted names such as the Ferret pseudo-variable names I, J, K, L, X, Y, Z, T, XBOX, YBOX, ZBOX, or TBOX, or them may include "illegal" characters such as "+", "-", "%", blanks, etc. To access such variable names in Ferret file simply enclose the name in single quotes. For example,
yes? PLOT 'x'
yes? CONTOUR 'SST from MP/RF measurements'
Pseudo-variables are variables whose values are coordinates or coordinate information from a grid. Valid pseudo-variables are
|
X – x axis coordinates |
I – x axis subscripts |
XBOX – size of x grid box |
|
Y – y axis coordinates |
J – y axis subscripts |
YBOX – size of y grid box |
|
Z – z axis coordinates |
K – z axis subscripts |
ZBOX – size of z grid box |
|
T – t axis coordinates |
L – t axis subscripts |
TBOX – size of t grid box |
A grid box is a concept needed for some transformations along an axis; it is the length along an axis that belongs to a single grid point and functions as a weighting factor during integrations and averaging transformations.
The pseudo-variables I, J, K, and L are subscripts; that is, they are a coordinate system for referring to grid locations in which the points along an axis are regarded as integers from 1 to the number of points on the axis. This is clear if you look at one of the sample data sets:
yes? USE levitus_climatology
yes? SHOW DATA
1> /home/e1/tmap/fer_dsets/descr/levitus_climatology.des
(default)
Levitus annual climatology (1x1 degree)
diagnostic
variables: NOT available
name title I
J K L
TEMP TEMPERATURE 1:360
1:180 1:20 ...
... on grid GLEVITR1 X=20E:20E(380) Y=90S:90N
Z=0m:5000m
SALT SALINITY 1:360 1:180
1:20 ...
... on grid GLEVITR1 X=20E:20E(380) Y=90S:90N Z=0m:5000m
We see that there are 20 points along the z-axis (1:20 under K), for example, and that the z-axis coordinate values range from 0 meters to 5000 meters. Pseudo-variables depend only on the underlying grid, and not on the variables (in this case, temperature and salt).
Examples: Pseudo-variables
1) yes? LIST/I=1:10 I
2) yes? LET xflux = u * vbox[G=u]
Ch3 Sec1.3.1. Grids and axes of pseudo-variables
The name of a pseudo-variable, alone, ("I", "T", "ZBOX", etc.) is not sufficient to determine the underlying axis of the pseudo-variable. The underlying axis may be specified explicitly, may be inherited from other variables used in the same expression, may be generated dynamically, or may be inherited from the current default grid. The following examples illustrate the possibilities:
TEMP + Y ! pseudo-variable Y inherits the y axis of variable TEMP
Y[G=TEMP] ! explicit: Y refers to the y axis of variable TEMP
Y[GY=axis_name] ! explicit: Y refers to axis axis_name
Y[Y=0:90:2] ! y axis is dynamically generated (See "dynamic axes">,
! p. 104)
In the expression
LET A = X + Y
in which the definition provides no explicit coaching, nor are there other variables from which Y can inherit an axis, the axis of Y will be inherited from the current default grid. The current default grid is specified by the SET GRID command and may be queried at any time with the SHOW GRID command. SHOW GRID will respond with "Default grid for DEFINE VARIABLE is grid".
Note that when pseudo-variables are buried within a user variable definition they do not inherit from variables used in conjunction with the user variable. For example, contrast these expressions involving pseudo-variable Y
USE coads_climatology ! has variable SST
LET A = Y ! Y buried inside variable A (axis indeterminate)
LIST SST + A ! y axis inherited from current default grid
LIST SST + Y ! y axis inherited from grid of SST
LIST SST + A[G=SST] ! y axis inherited from grid of SST
Ch3 Sec1.4. User-defined variables
New variables can be defined from existing variables and from abstract mathematical quantities (such as COS(latitude)) with command DEFINE VARIABLE (alias LET). The section later in this chapter, Defining New Variable (p. 100) expands on this capability.
See command DEFINE VARIABLE (p. 262) and command LET (p. 272) in the Commands Reference.
Examples: User-defined variables
1) yes? LET/TITLE="Surface Relief x1000 (meters)" r1000=rose/1000
2) yes?
LET/TITLE="Temperature Deviation" tdev=temp - temp[Z=@ave]
Ch3 Sec1.5. Abstract variables
Ferret can be used to manipulate abstract mathematical quantities such as SIN(x) or EXP(k*t)—quantities that are independent of file variable values. Such quantities are referred to as abstract expressions.
Example: Abstract variables
Contour the function
COS(a*Y)/EXP(b*T) where a=0.25 and b=-0.02
over the range
Y=0:45 (degrees) and T=1:100 (hours)
with a resolution of
0.5 degree on the Y axis and 2 hours on the T axis.
Quick and dirty solution:
yes? CONTOUR COS(0.25*Y[Y=0:45:0.5])/EXP(-0.2*T[T=1:100:2])
Nicer (Figure 3_1); plot is documented with correct units and titles):
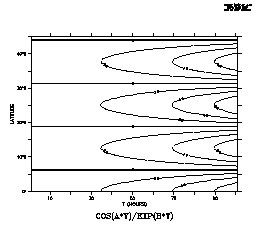yes? DEFINE AXIS/Y=0:45:0.5 /UNIT=DEGREES yaxSee the chapter "Grids and Regions", section "Grids" (p. 103), for more information on grids.
Ch3 Sec1.6. Missing value flags
Data values that are absent or undefined for mathematical reasons (e.g., 1/0) will be represented in Ferret with a missing value flag. In SHADE outputs a missing value flag embedded at some point in a variable will result in a transparent rectangular hole equal to the size of the grid cell of the missing value. In a CONTOUR or FILL plot it will result in a larger hole—extending past the grid box edge to the coordinate location of the next adjacent non-missing point—since contour lines cannot be interpolated between a missing value and its neighboring points. In the output of the LIST command for cases where the /FORMAT qualifier is not used the missing value will be represented by 4 dots ("...."). For cases where LIST/FORMAT=FORTRAN-format is used the numerical value of the missing value flag will be printed using the format provided.
Ch3 Sec1.6.1. Missing values in input files
Ferret does not impose a standard for missing value flags in input data sets; each variable in each data set may have its own distinct missing value flag(s). The flag(s) actually in use by a data set may be viewed with the SHOW DATA/VARIABLES command. If no missing value flag is specified for a data set Ferret will assume a default value of –1.E+34.
For EZ input data sets, either binary or ASCII, the missing data flag may be specified with the SET VARIABLE/BAD= command. A different value may be specified for each variable in the data set.
For NetCDF input data sets the missing value flag(s) is indicated by the values of the attributes "missing_value" and "_FillValue." If both attributes are defined to have different values both will be recognized and used by Ferret as missing value indicators, however the occurrences of _FillValue will be replaced with the value of missing_value as the data are read into Ferret's memory cache so that only a single missing value flag is apparent inside of Ferret. The command SET VARIABLE/BAD= can also be applied to NetCDF variables, thereby temporarily setting a user-imposed value for _FillValue.
Ch3 Sec1.6.2. Missing values in user-defined variables
User-defined variables may in general be defined as expressions involving multiple variables. The component variables need not in general agree in their choice of missing value flags. The result variable will inherit the bad value flag of the first variable in the expression. If the first component in the expression is a constant or a pseudo-variable, then Ferret imposes its default missing value flag of –1.E+34.
The function MISSING(variable,replacement) provides a limited control over the choice of missing values in user-defined variables. Note, however, that while the MISSING function will replace the missing values with other values it will not change the missing value flag. In other words, the replacement values will no longer be regarded as missing.
Ch3 Sec1.6.3. Missing values in output NetCDF files
Values flagged as missing inside Ferret will be faithfully transferred to output files—no substitution will occur as the data are written. In the case of NetCDF output files both of the attributes missing_value, and _FillValue will be set equal to the missing value flag.
Under some circumstances it is desirable to save a user-defined variable in a NetCDF file and then to redefine that variable and to append further output. (An example of this is the process of consolidating several files of input, say, moored measurements, into a gridded output.) The process of appending will not change any of the NetCDF attributes—neither long_name (title), units, nor missing_value or _FillValue. If the subsequent variable definitions do not agree in their choice of missing value flags the resulting output may contain multiple missing value flags that will not be properly documented.
An easy "trick" that avoids this situation is to begin all of the variable definitions with an addition of zero, "LET var = 0 + ...." The addition of zero will not affect the value of the output but it will guarantee that a missing value flag of –1.E+34 will be consistently used. Of course, you will want to use the SET VARIABLE/TITLE= command in conjunction with this approach.
Ch3 Sec1.6.4. Displaying the missing value flag
If the LIST command is used, missing values are, by default, displayed as "...." To examine the flag as a numerical value, use LIST/FORMAT=(E) (or some other suitable format).
Throughout this manual, Ferret commands that require and manipulate data are informally called "action" commands. These commands are:
PLOT
CONTOUR
FILL (alias for CONTOUR/FILL)
SHADE
VECTOR
POLYGON
WIRE
LIST
STAT
LOAD
Action commands may use any valid algebraic expression involving constants, operators (+,–,*,...), functions (SIN, MIN, INT,...), pseudo-variables (X, TBOX, ...) and other variables.
A variable name may optionally be followed by square brackets containing region, transformation, data set, and regridding qualifiers. For example, "temp", "salt[D=2]", "u[G=temp"], "u[Z=0:200@AVE]".
The expressions may also contain a syntax of:
IF condition THEN expression_1 ELSE expression_2
Examples: Expressions
i) temp ^ 2
temperature squared
ii) temp - temp[Z=@AVE]
for the range of Z in the current context, the temperature
deviations from the vertical average
iii) COS(Y)
the cosine of the Y coordinate of the underlying grid (by default,
the y-axis is implied by the other variables in the expression)
iv) IF (vwnd GT vwnd[D=monthly_navy_winds]) THEN vwnd ELSE 0
use the meridional
velocity from the current data set wherever it exceeds the value in data
set monthly_navy_winds, zero elsewhere.
Valid operators are
+
–
*
/
^ (exponentiate)
AND
OR
GT
GE
LT
LE
EQ
NE
Ch3 Sec2.2. Multi-dimensional expressions
Operators and functions (discussed in the next section, Functions) may combine variables of like dimensions or differing dimensions.
If the variables are of like dimension then the result of the combination is of the same dimensionality as inputs. For example, suppose there are two time series that have data on the same time axis; the result of a combination will be a time series on the same time axis.
If the variables are of unlike dimensionality, then the following rules apply:
1) To combine variables together in an expression they must be "conformable" along each axis.
2) Two variables are conformable along an axis if the number of points along the axis is the same, or if one of the variables has only a single point along the axis (or, equivalently, is normal to the axis).
3) When a variable of size 1 (a single point) is combined with a variable of larger size, the variable of size 1 is "promoted" by replicating its value to the size of the other variable.
4) If variables are the same size but have different coordinates, they are conformable, but Ferret will issue a message that the coordinates on the axis are ambiguous. The result of the combination inherits the coordinates of the FIRST variable encountered that has more than a single point on the axis.
Examples:
Assume a region J=50/K=1/L=1 for examples 1 and 2. Further assume that variables v1 and v2 share the same x-axis.
1) yes? LET newv = v1[I=1:10] + v2[I=1:10] !same dimension (10)
2) yes? LET newv = v1[I=1:10] + v2[I=5] !newv has length of v1 (10)
3) We want to compare the salt values during the first half of the year
with the values for the second half. Salt_diff will be placed on the time
coordinates of the first variable—L=1:6. Ferret will issue a warning about
ambiguous coordinates.
yes? LET salt_diff = salt[L=1:6] - salt[L=7:12]
4) In this example the variable zero will be promoted along each axis.
yes? LET zero = 0 * (i+j)
yes? LIST/I=1:5/J=1:5 zero !5X5 matrix
of 0's
5) Here we calculate density; salt and temp are on the same grid. This expression is an XYZ volume of points (100×100×10) of density at 10 depths based on temperature and salinity values at the top layer (K=1).
yes? SET REGION/I=1:100/J=1:100
yes? LET dens = rho_un (temp[K=1], salt[K=1],
Z[G=temp,K=1:10]
Functions are utilized with standard mathematical notation in Ferret. The arguments to functions are constants, constant arrays, pseudo-variables, and variables, possibly with associated qualifiers in square brackets, and expressions. Thus, all of these are valid function references:
A few functions also take strings as arguments. String arguments must be enclosed in double quotes. For example, a function to write variable "u" into a file named "my_output.v5d", formatted for the Vis5D program might be implemented as
You can list function names and argument lists with:
yes? SHOW FUNCTIONS ! List all functions
Yes? SHOW FUNCTIONS *TAN ! List all functions containing string
Valid functions are:
MAX(VAR) Compares two fields and selects the point by point maximum.
MAX(
temp[K=1], temp[K=2] ) returns the maximum temperature comparing the
first 2 z-axis levels.
MIN(VAR) Compares two fields and selects the point by point minimum.
MIN(
airt[L=10], airt[L=9] ) gives the minimum air temperature comparing two
timesteps.
INT (X) Truncates values to integers.
INT( salt ) returns the integer
portion of variable "salt" for all values in the current region.
ABS(X) absolute value.
ABS( U ) takes the absolute value of U for all
points within the current region
EXP(X) exponential ex; argument is real.
EXP( X ) raises e to the power
X for all points within the current region
LN(X) Natural logarithm logeX; argument is real.
LN( X ) takes the natural
logarithm of X for all points within the current region
LOG(X) Common logarithm log10X; argument is real.
LOG( X ) takes
the common logarithm of X for all points within the current region
SIN(THETA) Trigonometric sine; argument is in radians and is treated modulo
2*pi.
SIN( X ) computes the sine of X for all points within the current
region.
COS(THETA ) Trigonometric cosine; argument is in radians and is treated
modulo 2*pi.
COS( Y ) computes the cosine of Y for all points within the
current region
TAN(THETA) Trigonometric tangent; argument is in radians and is treated
modulo 2*pi.
TAN( theta ) computes the tangent of theta for all points
within the current region
ASIN(X) Trigonometric arcsine (-pi/2,pi/2) of X in radians.The result
will be flagged as missing if the absolute value of the argument is greater
than 1; result is in radians.
ASIN( value ) computes the arcsine of "value"
for all points within the current region
COS(X) Trigonometric arccosine (0,pi), in radians. The result will be
flagged as missing of the absolute value of the argument greater than 1;
result is in radians.
ACOS ( value ) computes the arccosine of "value"
for all points within the current region
ATAN(X) Trigonometric arctangent (-pi/2,pi/2); result is in radians.
ATAN(
value ) computes the arctangent of "value" for all points within the current
region
ATAN2(X,Y) 2-argument trigonometric arctangent of Y/X (-pi,pi); discontinuous
at Y=0.
ATAN2( X,Y ) computes the 2-argument arctangent of Y/X for all
points within the current region
MOD(A,B) Modulo operation ( arg1 – arg2*[arg1/arg2] ). Returns the remainder
when the first argument is divided by the second.
MOD( X,2 ) computes the
remainder of X/2 for all points within the current region
DAYS1900(year,month,day) computes the number of days since 1 Jan 1900.
This function is useful in converting dates to Julian days. If the year
is prior to 1900 a negative number is returned. This means that it is possible
to compute Julian days relative to, say, 1800 with the expression
LET jday1800
= DAYS1900 ( year, month, day) - DAYS1900( 1800,1,1)
MISSING(A,B) Replaces missing values in the first argument (multi-dimensional
variable) with the second argument; the second argument may be any conformable
variable.
MISSING( temp, -999 ) replaces missing values in temp with
–999
MISSING( sst, temp[D=coads_climatology] ) replaces missing sst values
with temperature from the COADS climatology
IGNORE0(VAR) Replaces zeros in a variable with the missing value flag for
that variable.
IGNORE0( salt ) replaces zeros in salt with the missing value
flag
RANDU(A) Generates a grid of uniformly distributed [0,1] pseudo-random
values. The first valid value in the field is used as the random number
seed. Values that are flagged as bad remain flagged as bad in the random
number field.
RANDU( temp[I=105:135,K=1:5] ) generates a field of uniformly
distributed random values of the same size and shape as the field "temp[I=105:135,K=1:5]"
using temp[I=105,k=1] as the pseudo-random number seed.
RANDN(A) Generates a grid of normally distributed pseudo-random values. As above, but normally distributed rather than uniformly distributed.
RHO_UN(SALT, TEMP, P) Calculates rho (density kg/m^3) from salt (psu),
temperature (deg C) and pressure (decibars) using the 1980 UNESCO International
Equation of State (IES80). The routine uses the high pressure equation
of state from Millero et al. (1980) and the oneatmosphere equation of state
from Millero and Poisson (1981) as reported in Gill (1982). The notation
follows Millero et al. (1980) and Millero and Poisson (1981).
RHO_UN( salt,
temp, Z )
THETA_FO(SALT, TEMP, Z, REF) Calculates local potential temperature field
at salt (psu), temperature (deg C), pressure (decibars) and specified reference
pressure. This calculation uses Bryden (1973) polynomial for adiabatic
lapse rate and Runge-Kutta 4th order integration algorithm. References:
Bryden, H., 1973, Deep-Sea Res., 20, 401–408; Fofonoff, N.M, 1977, Deep-Sea
Res., 24, 489–491.
THETA_FO( salt, temp, Z, Z_reference )
REASHAPE(A, B) The result of the RESHAPE function will be argument A "wrapped"
on the grid of argument B. The limits given on argument 2 are used to
specify subregions within the grid into which values should be reshaped.
RESHAPE(Tseries,MonthYear)
Two common uses of this function are to view multi-year time series data as a 2-dimensional field of 12-months vs. year and to map ABSTRACT axes onto real world coordinates. An example of the former is
DEFINE AXIS/t=15-JAN-1982:15-DEC-1985/NPOINTS=48/UNITS=DAYS tcal
LET my_time_series
= SIN(T[gt=tcal]/100)
! reshape 48 months into a 12 months by 4 year matrix
DEFINE AXIS/t=1982:1986:1 tyear
DEFINE AXIS/Z=1:12:1 zmonth
LET out_grid
= Z[GZ=zmonth]+T[GT=tyear]
LET my_reshaped = RESHAPE(my_time_series, out_grid)
SHOW
GRID my_reshaped
GRID (G001)
name axis # pts start
end
normal X
normal Y
ZMONTH Z 12
r 1 12
TYEAR T 5 r 1982
1986
For any axis X,Y,Z, or T if the axis differs between the input output grids, then limits placed upon the region of the axis in argument two (the output grid) can be used to restrict the geometry into which the RESHAPE is performed. Continuing with the preceding example:
! Now restrict the output region to obtain a 6 month by 8 year matrix
LIST RESHAPE(my_time_series,out_grid[k=1:6])
RESHAPE(MY_TIME_SERIES,OUT_GRID[K=1:6])
1 2 3 4 5 6
1
2 3 4 5 6
1982 / 1: 0.5144 0.7477 0.9123
0.9931 0.9827 0.8820
1983 / 2: 0.7003 0.4542 0.1665 -0.1366 -0.4271
-0.6783
1984 / 3: -0.8673 -0.9766 -0.9962 -0.9243 -0.7674 -0.5401
1985
/ 4: -0.2632 0.0380 0.3356 0.6024 0.8138 0.9505
1986 / 5: 0.9999
0.9575 0.8270 0.6207 0.3573 0.0610
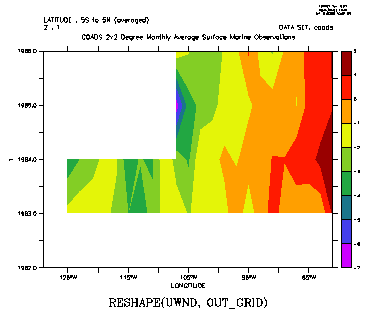
For any axis X,Y,Z, or T if the axis is the same in the input and output grids then the region from argument 1 will be preserved in the output. This implies that when the above technique is used on multi-dimensional input, only the axes which differ between the input and output grids are affected by the RESHAPE operation. The following filled contour plot of longitude by year number illustrates by expanding on the above example: (Figure 3_2)
! The year-by-year progression January winds for a longitudinal patch
!
averaged from 5s to 5n across the eastern Pacific Ocean. Note that
!
k=1 specifies January, since the Z axis is month
USE coads
LET out_grid = Z[GZ=zmonth]+T[GT=tyear]+X[GX=uwnd]+Y[GY=uwnd]
LET
uwnd_mnth_ty = RESHAPE(uwnd, out_grid)
FILL uwnd_mnth_ty[X=130W:80W,Y=5S:5N@AVE,K=1]
In the second usage mentioned, to map ABSTRACT axes onto real world coordinates,
suppose xpts and ypts contain time series of length Nt points representing
longitude and latitude points along an oceanographic ship track and the
variable global_sst contains global sea surface temperature data. Then
the result of
LET sampled_sst = SAMPLEXY(global_sst, xpts, ypts)
will be a 1-dimensional grid: Nt points along the XABSTRACT axis. The RESHAPE function can be used to remap this data to the original time axis using
RESHAPE(sampled_sst, xpts)
LET sampled_sst = SAMPLEXY(global_sst,
Xpts[t=1-jan-1980:15-jan-1980],
ypts[t=1-jan-1980:15-jan-1980])
RESHAPE(sampled_sst,
xpts[t=1-jan-1980:15-jan-1980])
When the input and output grids share any of the same axes, then the specified sub-region along those axes will be preserved in the RESHAPE operation. In the example "RESHAPE(myTseries,myMonthYearGrid)" this means that if myTseries and myMonthYearGrid were each multidimensional variables with the same latitude and longitude grids then
RESHAPE(myTseries[X=130E:80W,Y=5S:5N],myMonthYearGrid)
would map onto the X=130E:80W,Y=5S:5N sub-region of the grid of myMonthYearGrid. When the input and output axes differ the sub-region of the output that is utilized may be controlled by inserting explicit limit qualifiers on the second argument
ZAXREPLACE(V,ZVALS,ZAX) Convert between alternative monotonic Zaxes, where
the mapping between the source and destination Z axes is a function of
X,Y, and or T. Typical applications in the field of oceanography include
converting from a Z axis of layer number to a Z axis in units of depth
(e.g., for sigma coordinate fields) and converting from a Z axes of depth
to one of density (for a stably stratified fluid).
Argument 1, V, is the
field of data values, say temperature on the "source" Z-axis, say, layer
number. The second argument, ZVALS, contains values in units of the desired
destination Z axis (ZAX) on the Z axis as V — for example, depth values
associated with each vertical layer. The third argument, ZAX, is any variable
defined on the destination Z axis, often "Z[gz=zaxis_name]" is used. For
example:
Contour salt as a function of density:
yes? set dat ocean_atlas_annual
!
Define density sigma, then density axis axden
yes? let sigma=rho_un(salt,temp,0)-1000
yes?
define axis/z=21:28:.05 axden
! Regrid to density
yes? let saltonsigma= ZAXREPLACE(
salt, sigma, z[gz=axdens])
! MakePacific plot
yes? fill/y=0/x=120e:75w/yli=28:21:-1
saltonsigma
Ch3 Sec2.3.25. XSEQUENCE, YSEQUENCE, ZSEQUENCE, TSEQUENCE
XSEQUENCE(A), YSEQUENCE(A), ZSEQUENCE(A), TSEQUENCE(A) Unravels the data from the argument into a 1-dimensional line of data on an ABSTRACT axis.
FFTA(A) Computes fft amplitude spectra, normalized by 1/N
|
Arguments: |
A |
Variable with regular time axis. |
|
Result Axes: |
X |
Inherited from A |
|
Y |
Inherited from A |
|
|
Z |
Inherited from A |
|
|
T |
Generated by the function: frequency in cyc/(time units from A) |
See the demonstration script ef_fft_demo.jnl for an example using this function.
FFTA returns a(j) in
f(t) = S(j=1 to N/2)[a(j) cos(jwt + F(j))]
where [ ] means "integer part of", w=2 pi/T is the fundamental frequency, and T=N*Dt is the time span of the data input to FFTA. F is the phase (returned by FFTP, see next section)
The units of the returned time axis are "cycles/Dt" where Dt is the time increment.
Even and odd N's are allowed. N need not be a power of 2. FFTA and FFTP assume f(1)=f(N+1), and the user gives the routines the first N pts.
The code is based on the FFT routines in Swarztrauber's FFTPACK available at www.netlib.org.
FFTP(A) Computes fft phase
|
Arguments: |
A |
Variable with regular time axis. |
|
Result Axes: |
X |
Inherited from A |
|
Y |
Inherited from A |
|
|
Z |
Inherited from A |
|
|
T |
Generated by the function: frequency in cyc/(time units from A) |
See the demonstration script ef_fft_demo.jnl for an example using this function.
FFTP returns F(j) in
f(t) = S(j=1 to N/2)[a(j) cos(jwt + F(j))]
where [ ] means "integer part of", w=2 pi/T is the fundamental frequency, and T=N*Dt is the time span of the data input to FFTA.
The units of the returned time axis are "cycles/Dt" where Dt is the time increment.
Even and odd N's are allowed. Power of 2 not required. FFTA and FFTP assume f(1)=f(N+1), and the user gives the routines the first N pts.
The code is based on the FFT routines in Swarztrauber's FFTPACK available at www.netlib.org.
SAMPLEI(TO_BE_SAMPLED,X_INDICES) samples a field at a list of X indices, which are a subset of its X axis
|
Arguments: |
TO_BE_SAMPLED |
Data to sample |
|
X_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
ABSTRACT; length same as X_INDICES |
|
Y |
Inherited from TO_BE_SAMPLED |
|
|
Z |
Inherited from TO_BE_SAMPLED |
|
|
T |
Inherited from TO_BE_SAMPLED |
See the demonstration ef_sort_demo.jnl for a common useage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call, e.g.
yes? LET sampled_data = samplei(airt[X=160E:180E], xindices)
SAMPLEJ(TO_BE_SAMPLED,Y_INDICES) samples a field at a list of Y indices, which are a subset of its Y axis
|
Arguments: |
TO_BE_SAMPLED |
Data to be sample |
|
Y_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
Inherited from TO_BE_SAMPLED |
|
Y |
ABSTRACT; length same as Y_INDICES |
|
|
Z |
Inherited from TO_BE_SAMPLED |
|
|
T |
Inherited from TO_BE_SAMPLED |
See the demonstration ef_sort_demo.jnl for a common useage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call.
SAMPLEK(TO_BE_SAMPLED, Z_INDICES) samples a field at a list of Z indices, which are a subset of its Z axis
|
Arguments: |
TO_BE_SAMPLED |
Data to sample |
|
Z_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
Inherited from TO_BE_SAMPLED |
|
Y |
Inherited from TO_BE_SAMPLED |
|
|
Z |
ABSTRACT; length same as Z_INDICES |
|
|
T |
Inherited from TO_BE_SAMPLED |
See the demonstration ef_sort_demo.jnl for a common useage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call.
SAMPLEL(TO_BE_SAMPLED, T_INDICES) samples a field at a list of T indices, a subset of its T axis
|
Arguments: |
TO_BE_SAMPLED |
Data to sample |
|
T_INDICES |
list of indices of the variable TO_BE_SAMPLED |
|
|
Result Axes: |
X |
Inherited from TO_BE_SAMPLED |
|
Y |
Inherited from TO_BE_SAMPLED |
|
|
Z |
Inherited from TO_BE_SAMPLED |
|
|
T |
ABSTRACT; length same as X_INDICES |
See the demonstration ef_sort_demo.jnl for a common useage of this function. As with other functions which change axes, specify any region information for the variable TO_BE_SAMPLED explicitly in the function call.
SAMPLEIJ(DAT_TO_SAMPLE,XPTS,YPTS) Returns data sampled at a subset of its grid points, defined by (XPTS, YPTS)
|
Arguments: |
DAT_TO_SAMPLE |
Data to sample, field of x, y, and perhaps z and t |
|
XPTS |
X indices of grid points |
|
|
YPTS |
Y indices of grid points |
|
|
Result Axes: |
X |
ABSTRACT, length of list (xpts,ypts) |
|
Y |
NORMAL (no axis) |
|
|
Z |
Inherited from DAT_TO_SAMPLE |
|
|
T |
Inherited from DAT_TO_SAMPLE |
SAMPLET_DATE (DAT_TO_SAMPLE, YR, MO, DAY, HR, MIN, SEC) Returns data sampled by interpolating to one or more times
|
Arguments: |
DAT_TO_SAMPLE |
Data to sample, field of x, y, z and t |
|
YR |
Year(s), integer YYYY |
|
|
MO |
Month(s), integer month number MM |
|
|
DAY |
Day(s) of month, integer DD |
|
|
HR |
Hour(s) integer HH |
|
|
MIN |
Minute(s), integer MM |
|
|
SEC |
Second(s), integer SS |
|
|
Result Axes: |
X |
Inherited from DAT_TO_SAMPLE |
|
Y |
Inherited from DAT_TO_SAMPLE |
|
|
Z |
Inherited from DAT_TO_SAMPLE |
|
|
T |
ABSTRACT; length is # times sampled |
Example:
List wind speed at a subset of points from the COADS data set
yes? USE coads
yes? SET REGION/X=131E:135E/Y=39N
yes? LET my_wspd = samplet_date(wspd,{1986,1986},{5,8},{16,15},{12,12},{0,0},{0,
0})
yes? LIST my_wspd
SAMPLET_DATE(WSPD,{1986,1986},{5,8},{16,15},{12,12},{0,0},{0,0})
LATITUDE: 39N
DATA SET: /home/shiva/data/coads.cdf
131E 133E 135E
56 57 58
1 / 1: 5.130
4.690 5.120
2 / 2: 5.267 4.962 4.666
SAMPLEXY(DAT_TO_SAMPLE,XPTS,YPTS) Returns data sampled at a set of (X,Y) points, using linear interpolation
|
Arguments: |
DAT_TO_SAMPLE |
Data to sample |
|
XPTS |
X values of sample points |
|
|
YPTS |
Y values of sample points |
|
|
Result Axes: |
X |
ABSTRACT; length same as XPTSand YPTS |
|
Y |
NORMAL (no axis) |
|
|
Z |
Inherited from DAT_TO_SAMPLE |
|
|
T |
Inherited from DAT_TO_SAMPLE |
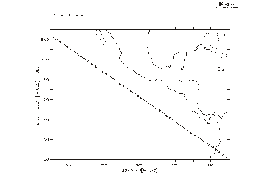
Example:
Plot a section of data taken along a slanted line in the Pacific (Figure3_3a). One could use a ship track, specifying its coordinates as xlon, ylat.
yes? USE ocean_atlas_annual
yes? LET xlon = 234.5 + I[I=1:50] ! define
the slant line
yes? LET dely = 24./49
yes? LET ylat = 24.5 - dely*i[i=1:50]
+ dely
yes? PLOT/VS/LINE/SYM=27 xlon,ylat ! line off Central America
yes?
GO land
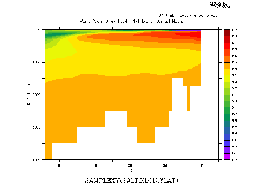
Now sample the field "salt" along this track and make a filled contour plot. The horizontal axis is abstract; it is a count of the number of points along the track. (Figure3_3b)
yes? LET slantsalt = samplexy(salt,xlon,ylat)
yes? FILL/LEVELS=(33.2,35.2,0.1)/VLIMITS=0:4000
slantsalt
Ch3 Sec2.3.35.
SCAT2GRIDGAUSS_XY
SCAT2GRIDGAUSS_XY(XPTS, YPTS, F, XAX, YAX, XSCALE, YSCALE, XCUTOFF, YCUTOFF) Use Gaussian weighting to grid scattered data to an XY grid
|
Arguments: |
XPTS |
x-coordinates of scattered input triples; may be fcn of time |
|
YPTS |
y-coordinates of scattered input triples; may be fcn of time |
|
|
F |
F(X,Y) 3rd component of scattered input triples. May be fcn of time |
|
|
XAX |
X-axis of output grid |
|
|
YAX |
Y-axis of output grid |
|
|
XSCALE |
Radius of influence in the X direction, in data units (e.g. lon or m) |
|
|
YSCALE |
Radius of influence in the Y direction, in data units (e.g. lon or m) |
|
|
XCUTOFF |
Cutoff for weight function in the X direction. Cutoff = 2 means the minimum weightweight is e-4 |
|
|
YCUTOFF |
Cutoff for weight function in the Y directionCutoff = 2 means the minimum weightweight is e-4 |
|
|
Result Axes: |
X |
Inherited from XAX |
|
Y |
Inherited from YAX |
|
|
Z |
NORMAL (no axis) |
|
|
T |
Inherited from F |
The scat2gridgauss* functions use a Gaussian interpolation method map irregular locations (xn, yn) to a regular grid (x0, y0).
Parameters for a square grid and a fairly dense distribution of scattered points relative to the grid might be XSCALE=YSCALE = 0.5, and XCUTOFF=YCUTOFF = 2. To get better coverage, use a coarser grid or increase XSCALE, YSCALE and/or XCUTOFF, YCUTOFF.
The value of the gridded function F at each grid point (x0, y0) is computed by:
F(x0,y0) = S(n=1 to Np)F(xn,yn)W(xn,yn) / S(n=1 to Np)W(xn,yn)
Where Np is the total number of irregular points within the "influence region" of a particular grid point, (determined by the CUTOFF parameters, defined below). The Gaussian weight fucntion Wn is given by
Wn(xn,yn) = exp{-[(xn-x0)2/X2 + (yn-y0)2/Y2]}
X and Y in the denominators on the right hand side are the mapping scales, arguments 6 and 7.
The weight function has a nonzero value everywhere, so all of the scattered points in theory could be part of the sum for each grid point. To cut computation, the parameters XCUTOFF and YCUTOFFf are employed. If a cutoff of 2 is used, then scattered points with Wn< e-4. This occurs where distances from the grid point are less than 2 times the mapping scales X or Y.
(Reference for this method: Kessler and McCreary, 1993: The Annual Wind-driven Rossby Wave in the Subthermocline Equatorial Pacivif, Journal of Physical Oceanography 23, 1192 -1207)
Ch3 Sec2.3.36. SCAT2GRIDGAUSS_XZ
SCAT2GRIDGAUSS_XZ(XPTS, ZPTS, F, XAX, ZAX, XSCALE, ZSCALE, XCUTOFF, ZCUTOFF) Use Gaussian weighting to grid scattered data to an XZ grid
|
Arguments: |
XPTS |
x-coordinates of scattered input triples; may be fcn of time |
|
ZPTS |
z-coordinates of scattered input triples; may be fcn of time |
|
|
F |
F(X,Z) 3rd component of scattered input triples. May be fcn of time |
|
|
XAX |
X-axis of output grid |
|
|
ZAX |
Z-axis of output grid |
|
|
XSCALE |
Radius of influence in the X direction, in data units (e.g. lon or m) |
|
|
ZSCALE |
Radius of influence in the Z direction, in data units (e.g. lon or m) |
|
|
XCUTOFF |
Cutoff for weight function in the X direction. Cutoff = 2 means the minimum weightweight is e-4 |
|
|
ZCUTOFF |
Cutoff for weight function in the Z direction. Cutoff = 2 means the minimum weightweight is e-4 |
|
|
Result Axes: |
X |
Inherited from XAX |
|
Y |
NORMAL (no axis) |
|
|
Z |
Inherited from ZAX |
|
|
T |
Inherited from F |
See the discussion under SCAT2GRIDGAUSS_XY (p. 68)
Ch3 Sec2.3.37. SCAT2GRIDGAUSS_XY
SCAT2GRIDGAUSS_XY(YPTS, zPTS, F, YAX, ZAX, YSCALE, ZSCALE, YCUTOFF, ZCUTOFF) Use Gaussian weighting to grid scattered data to a YZ grid
|
Arguments: |
YPTS |
y-coordinates of scattered input triples; may be fcn of time |
|
ZPTS |
z-coordinates of scattered input triples; may be fcn of time |
|
|
F |
F(Y,Z) 3rd component of scattered input triples. May be fcn of time |
|
|
YAX |
Y-axis of output grid |
|
|
ZAX |
Z-axis of output grid |
|
|
YSCALE |
Radius of influence in the Y direction, in data units (e.g. lon or m) |
|
|
ZSCALE |
Radius of influence in the Z direction, in data units (e.g. lon or m) |
|
|
YCUTOFF |
Cutoff for weight function in the Y direction. Cutoff = 2 means the minimum weightweight is e-4 |
|
|
ZCUTOFF |
Cutoff for weight function in the Y directionCutoff = 2 means the minimum weightweight is e-4 |
|
|
Result Axes: |
X |
NORMAL (no axis) |
|
Y |
Inherited from YAX |
|
|
Z |
Inherited from ZAX |
|
|
T |
Inherited from F |
See the discussion under SCAT2GRIDGAUSS_XY (p. 68)
Ch3 Sec2.3.38. SCAT2GRIDLAPLACE_XY
SCAT2GRIDLAPLACE_XY(XPTS, YPTS, F, XAX, YAX, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to an XY grid.
|
Arguments: |
XPTS |
x-coordinates of scattered input triples. May be fcn of time |
|
YPTS |
y-coordinates of scattered input triples. May be fcn of time |
|
|
F |
F(X,Y) 3rd component of scattered input triples. May be fcn of time |
|
|
XAX |
X-axis of output grid |
|
|
YAX |
Y-axis of output grid |
|
|
CAY |
Amount of spline eqation (between 0 and inf.) vs Laplace interpolation |
|
|
NRNG |
Grid points more than NRNG grid spaces from the nearest data point are set to undefined. |
|
|
Result Axes: |
X |
Inherited from XAX |
|
Y |
Inherited from YAX |
|
|
Z |
NORMAL (no axis) |
|
|
T |
Inherited from F |
The SCAT2GRIDLAPLACE* functions employ the same interpolation method as is used by PPLUS, and appears elsewhere in Ferret, e.g. in contouring. The parameters are used as follows (quoted from the PPLUS Users Guide):
CAY
If CAY=0.0, Laplacian interpolation is used. The resulting surface
tends to have rather sharp peaks and dips at the data points (like a tent
with poles pushed up into it). There is no chance of spurious peaks appearing.
As CAY is increased, Spline interpolation predominates over the Laplacian,
and the surface passes through the data points more smoothly. The possibility
of spurious peaks increases with CAY. CAY= infinity is pure Spline interpolation.
An over relaxation process in used to perform the interpolation. A
value of CAY=5 often gives a good surface.
NRNG
Any grid points farther than NRNG away from the nearest data point
will be set to "undefined" The default used by PPLUS is NRNG = 5
Ch3 Sec2.3.39. SCAT2GRIDLAPLACE_XZ
SCAT2GRIDLAPLACE_XZ(XPTS, ZPTS, F, XAX, ZAX, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to an XZ grid.
|
Arguments: |
XPTS |
x-coordinates of scattered input triples. May be fcn of time |
|
ZPTS |
z-coordinates of scattered input triples. May be fcn of time |
|
|
F |
F(X,Z) 3rd component of scattered input triples. May be fcn of time |
|
|
XAX |
X-axis of output grid |
|
|
ZAX |
Z-axis of output grid |
|
|
CAY |
Amount of spline eqation (between 0 and inf.) vs Laplace interpolation |
|
|
NRNG |
Grid points more than NRNG grid spaces from the nearest data point are set to undefined. |
|
|
Result Axes: |
X |
Inherited from XAX |
|
Y |
NORMAL (no axis) |
|
|
Z |
Inherited from ZAX |
|
|
T |
Inherited from F |
See the discussion under SCAT2GRIDLAPLACE_XY (p. 72)
Ch3 Sec2.3.40. SCAT2GRIDLAPLACE_YZ
SCAT2GRIDLAPLACE_YZ(YPTS, ZPTS, F, YAX, ZAX, CAY, NRNG) Use Laplace/ Spline interpolation to grid scattered data to an YZ grid.
|
Arguments: |
YPTS |
y-coordinates of scattered input triples. May be fcn of time |
|
ZPTS |
z-coordinates of scattered input triples. May be fcn of time |
|
|
F |
F(Y,Z) 3rd component of scattered input triples. May be fcn of time |
|
|
YAX |
Y-axis of output grid |
|
|
ZAX |
Z-axis of output grid |
|
|
CAY |
Amount of spline eqation (between 0 and inf.) vs Laplace interpolation |
|
|
NRNG |
Grid points more than NRNG grid spaces from the nearest data point are set to undefined. |
|
|
Result Axes: |
X |
NORMAL (no axis) |
|
Y |
Inherited from YAX |
|
|
Z |
Inherited from ZAX |
|
|
T |
Inherited from F |
See the discussion under SCAT2GRIDLAPLACE_XY (p. 73)
SORTI(DAT): Returns indices of data, sorted on the I axis in increasing order
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
ABSTRACT, same length as DAT x-axis |
|
Y |
Inherited from DAT |
|
|
Z |
Inherited from DAT |
|
|
T |
Inherited from DAT |
SORTI, SORTJ, SORTK, and SORTL return the indices of the data after it has been sorted. These functions are used in conjunction with functions such as the SAMPLE functions to do sorting and sampling. See the demonstration ef_sort_demo.jnl for common useage of these functions.
SORTJ(DAT) Returns indices of data, sorted on the I axis in increasing order
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
Inherited from DAT |
|
Y |
ABSTRACT, same length as DAT y-axisInherited from DAT |
|
|
Z |
Inherited from DAT |
|
|
T |
Inherited from DAT |
SORTI, SORTJ, SORTK, and SORTL return the indices of the data after it has been sorted. These functions are used in conjunction with functions such as the SAMPLE functions to do sorting and sampling. See the demonstration ef_sort_demo.jnl for common useage of these functions.
SORTK(DAT) Returns indices of data, sorted on the I axis in increasing order
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
Inherited from DAT |
|
Y |
Inherited from DAT |
|
|
Z |
ABSTRACT, same length as DAT x-axis |
|
|
T |
Inherited from DAT |
SORTI, SORTJ, SORTK, and SORTL return the indices of the data after it has been sorted. These functions are used in conjunction with functions such as the SAMPLE functions to do sorting and sampling. See the demonstration ef_sort_demo.jnl for common useage of these functions.
SORTL(DAT) Returns indices of data, sorted on the L axis in increasing order
|
Arguments: |
DAT |
DAT: variable to sort |
|
Result Axes: |
X |
Inherited from DAT |
|
Y |
Inherited from DAT |
|
|
Z |
Inherited from DAT |
|
|
T |
ABSTRACT, same length as DAT x-axis |
SORTI, SORTJ, SORTK, and SORTL return the indices of the data after it has been sorted. These functions are used in conjunction with functions such as the SAMPLE functions to do sorting and sampling. See the demonstration ef_sort_demo.jnl for common useage of these functions.
TAUTO_COR: (beta) Compute autocorrelation function (ACF) of time series, lags of 0,...,N-1
Transformations (e.g., averaging, integrating, etc.) may be specified along the axes of a variable. Some transformations (e.g., averaging) reduce a range of data to a point; others (e.g., differentiating) retain the range.
When transformations are specified along more than one axis of a single variable the order of execution is X axis first, then Y then Z then T.
The regridding transformations are described in the chapter "Grids and Regions" (p. 103).
Example syntax: TEMP[Z=0:100@LOC:20] (depth at which temp has value 20)
Valid transformations are
|
|
Default |
|
|
@DIN |
definite integral (weighted sum) |
|
|
@IIN |
indefinite integral (weighted running sum) |
|
|
@AVE |
average |
|
|
@VAR |
unweighted variance |
|
|
@MIN |
minimum |
|
|
@MAX |
maximum |
|
|
@SHF |
1 pt |
shift |
|
@SBX |
3 pt |
boxcar smoothed |
|
@SBN |
3 pt |
binomial smoothed |
|
@SHN |
3 pt |
Hanning smoothed |
|
@SPZ |
3 pt |
Parzen smoothed |
|
@SWL |
3 pt |
Welch smoothed |
|
@DDC |
centered derivative |
|
|
@DDF |
forward derivative |
|
|
@DDB |
backward derivative |
|
|
@NGD |
number of valid points |
|
|
@NBD |
number of bad (invalid) points flagged |
|
|
@SUM |
unweighted sum |
|
|
@RSUM |
running unweighted sum |
|
|
@FAV |
3 pt |
fill missing values with average |
|
@FLN:n |
1 pt |
fill missing values by linear interpolation |
|
@FNR:n |
1 pt |
fill missing values with nearest point |
|
@LOC |
0 |
coordinate of ... (e.g., depth of 20 degrees) |
|
@WEQ |
"weighted equal" (integrating kernel) |
|
|
@CDA |
closest distance above |
|
|
@CDB |
closest distance below |
|
|
@CIA |
closest index above |
|
|
@CIB |
closest index below |
The command SHOW TRANSFORM will produce a list of currently available transformations.
|
U[Z=0:100@AVE] |
– average of u between 0 and 100 in Z |
|
sst[T=@SBX:10] |
– box-car smooths sst with a 10 time point filter |
|
tau[L=1:25@DDC] |
– centered time derivative of tau |
|
v[L=@IIN] |
– indefinite (accumulated) integral of v |
|
qflux[X=@AVE,Y=@AVE] |
– XY area-averaged qflux |
Ch3 Sec2.4.1. General information about transformations
Transformations are normally computed axis by axis; if multiple axes have transformations specified simultaneously (e.g., U[Z=@AVE,L=@SBX:10]) the transformations will be applied sequentially in the order X then Y then Z then T. There are two exceptions to this: if @DIN is applied simultaneously to both the X and Y axes (in units of degrees of longitude and latitude, respectively) the calculation will be carried out on a per-unit-area basis (as a true double integral) instead of a per-unit-length basis, sequentially. This ensures that the COSINE(latitude) factors will be applied correctly. The same applies to @AVE simultaneously on X and Y.
Data that are flagged as invalid are excluded from calculations.
When calculating integrals and derivatives (@IIN, @DIN, @DDC, @DDF, and @DDB) Ferret attempts to use standardized units for the grid coordinates. If the underlying axis is in a known unit of length Ferret converts grid box lengths to meters. If the underlying axis is in a known unit of time Ferret converts grid box lengths to seconds. If the underlying axis is degrees of longitude a factor of COSINE (latitude) is applied to the grid box lengths in meters.
If the underlying axis units are unknown Ferret uses those unknown units for the grid box lengths. (If Ferret does not recognize the units of an axis it displays a message to that effect when the DEFINE AXIS or SET DATA command defines the axis.) See command DEFINE AXIS/UNITS (p. 257) in the Commands Reference in this manual for a list of recognized units.
All integrations and averaging are accomplished by multiplying the width of each grid box by the value of the variable in that grid box—then summing and dividing as appropriate for the particular transformation.
If integration or averaging limits are given as world coordinates, the grid boxes at the edges of the region specified are weighted according to the fraction of grid box that actually lies within the specified region. If the transformation limits are given as subscripts, the full box size of each grid point along the axis is used—including the first and last subscript given. The region information that is listed with the output reflects this.
Some transformations (derivatives, shifts, smoothers) require data points from beyond the edges of the indicated region in order to perform the calculation. Ferret automatically accesses this data as needed. It flags edge points as missing values if the required beyond-edge points are unavailable (e.g., @DDC applied on the X axis at I=1).
Ch3 Sec2.4.2. Transformations applied to irregular regions
Since transformations are applied along the orthogonal axes of a grid they lend themselves naturally to application over "rectangular" regions (possibly in 3 or 4 dimensions). Ferret has sufficient flexibility, however, to perform transformations over irregular regions.
Suppose, for example, that we wish to determine the average wind speed within an irregularly shaped region of the globe defined by a threshold sea surface temperature value. We can do this through the creation of a mask, as in this example:
yes? SET DATA coads_climatology
yes? SET REGION/l=1/@t ! January
in the Tropical Pacific
yes? LET sst28_mask = IF sst GT 28 THEN 1
yes? LET
masked_wind_speed = wspd * sst28_mask
yes? LIST masked_wind_speed[X=@AVE,Y=@AVE]
The variable sst28_mask is a collection of 1's and missing values. Using it as a multiplier on the wind speed field produces a new result that is undefined except in the domain of interest.
When using masking be aware of these considerations:
Ch3 Sec2.4.3. General information about smoothing transformations
Ferret provides several transformations for smoothing variables (removing high frequency variability). These transformations replace each value on the grid to which they are applied with a weighted average of the surrounding data values along the axis specified. For example, the expression u[T=@SPZ:3] replaces the value at each (I,J,K,L) grid point of the variable "u" with the weighted average
u at t = 0.25*(u at t-1) + 0.5*(u at t) + 0.25*(u at t+1)
The various choices of smoothing transformations (@SBX, @SBN, @SPZ, @SHN, @SWL) represent different shapes of weighting functions or "windows" with which the original variable is convolved. New window functions can be obtained by nesting the simple ones provided. For example, using the definitions
yes? LET ubox = u[L=@SBX:15]
yes? LET utaper = ubox[L=@SHN:7]
produces a 21-point window whose shape is a boxcar (constant weight) with COSINE (Hanning) tapers at each end.
Ferret may be used to directly examine the shape of any smoothing window: Mathematically, the shape of the smoothing window can be recovered as a variable by convolving it with a delta function. In the example below we examine (PLOT) the shape of a 15-point Welch window (Figure 3_4).
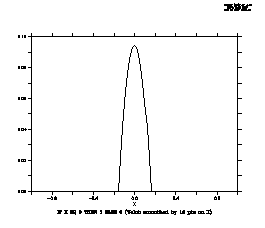! define X axis as [-1,1] by 0.2Ch3 Sec2.4.4. @DIN—definite integral
The transformation @DIN computes the definite integral—a single value that is the integral between two points along an axis (compare with @IIN). It is obtained as the sum of the grid_box*variable product at each grid point. Grid points at the ends of the indicated range are weighted by the fraction of the grid box that falls within the integration interval.
If @DIN is specified simultaneously on multiple axes the calculation will be performed as a multiple integration rather than as sequential single integrations. The output will document this fact by indicating a transformation of "@IN4" or "XY integ." See General Information (p 76) for important details about this transformation.
Example:
yes? CONTOUR/X=160E:160W/Y=5S:5N u[Z=0:50@DIN]
In a latitude/longitude coordinate system X=@DIN is sensitive to the COS(latitude) correction.
Integration over complex regions in space may be achieved by masking the multi-dimensional variable in question and using the multi-dimensional form of @DIN. For example
yes? LET salinity_where_temp_gt_15 = IF temp GT 15 THEN salt
yes? LIST
salinity_where_temp_gt_15[X=@DIN,Y=@DIN,Z=@DIN]
Ch3 Sec2.4.5. @IIN—indefinite integral
The transformation @IIN computes the indefinite integral—at each subscript of the result it is the value of the integral from the start value to the upper edge of that grid box. It is obtained as a running sum of the grid_box*variable product at each grid point. Grid points at the ends of the indicated range are weighted by the fraction of the grid box that falls within the integration interval. See General Information (p 76) for important details about this transformation.
Example:
yes? CONTOUR/X=160E:160W/Z=0 u[Y=5S:5N@IIN]
Note 1: The indefinite integral is always computed in the increasing coordinate direction. To compute the indefinite integral in the reverse direction use
LET reverse_integral = my_var[Y=lo:hi@DIN] - my_var[X=lo:hi@IIN]
Note 2: In a latitude/longitude coordinate system X=@IIN is sensitive to the COS(latitude) correction.
Note 3: The result of the indefinite integral is shifted by 1/2 of a grid cell from its "proper" location. This is because the result at each grid cell includes the integral computed to the upper end of that cell. (This was necessary in order that var[I=lo:hi@DIN] and var[I=lo:hi@IIN] produce consistent results.)
To illustrate, consider these commands
yes? LET one = x-x+1
yes? LIST/I=1:3 one[I=@din]
X-X+1
X: 0.5 to 3.5 (integrated)
3.000
yes? LIST/I=1:3 one[I=@iin]
X-X+1
indef. integ. on X
1 / 1: 1.000
2 /
2: 2.000
3 / 3: 3.000
The grid cell at I=1 extends from 0.5 to 1.5. The value of the integral at 1.5 is 1.000 as reported but the coordinate listed for this value is 1 rather than 1.5. Two methods are available to correct for this 1/2 grid cell shift.
Method 1: correct the result by subtracting the 1/2 grid cell error
yes? LIST/I=1:3 one[I=@iin] - one/2
ONE[I=@IIN] - ONE/2
1
/ 1: 0.500
2 / 2: 1.500
3 / 3: 2.500
Method 2: correct the coordinates by shifting the axis 1/2 of a grid cell
yes? DEFINE AXIS/X=1.5:3.5:1 xshift
yes? LET SHIFTED_INTEGRAL = one[I=@IIN]
yes?
LET corrected_integral = shifted_integral[GX=xshift@ASN]
yes? LIST/I=1:3
corrected_integral
SHIFTED_INTEGRAL[GX=XSHIFT@ASN]
1.5 / 1:
1.000
2.5 / 2: 2.000
3.5 / 3: 3.000
The transformation @AVE computes the average weighted by grid box size—a single number representing the average of the variable between two endpoints.
If @AVE is specified simultaneously on multiple axes the calculation will be performed as a multiple integration rather than as sequential single integrations. The output will document this fact by showing @AV4 or "XY ave" as the transformation. See General Information (p 76) for important details about this transformation.
Example:
yes? CONTOUR/X=160E:160W/Y=5S:5N u[Z=0:50@AVE]
Note that the unweighted mean can be calculated using the @SUM and @NGD transformations.
Averaging over complex regions in space may be achieved by masking the multi-dimensional variable in question and using the multi-dimensional form of @AVE. For example
yes? LET salinity_where_temp_gt_15 = IF temp GT 15 THEN salt
yes? LIST salinity_where_temp_gt_15[X=@AVE,Y=@AVE,Z=@AVE]
Ch3 Sec2.4.7. VAR—weighted variance
The transformation @VAR computes the weighted variance of the variable with respect to the indicated region (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986).
As with @AVE, if @VAR is applied simultaneously to multiple axes the calculation is performed as the variance of a block of data rather than as nested 1-dimensional variances. See General Information (p 76) for important details about this transformation.
The transformation @MIN finds the minimum value of the variable within the specified axis range. See General Information (p 76) for important details about this transformation.
Example:
For fixed Z and Y
yes? PLOT/T="1-JAN-1982":"1-JAN-1983" temp[X=160E:160W@MIN]
plots a time series of the minimum temperature found between longitudes 160 east and 160 west.
The transformation @MAX finds the maximum value of the variable within the specified axis range. See also @MIN. See General Information (p 76) for important details about this transformation.
The transformation @SHF shifts the data up or down in subscript by the number of points given as the argument. See General Information (p 76) for important details about this transformation.
Examples:
U[L=@SHF:2]
associates the value of U[L=3] with the subscript L=1.
U[L=@SHF:1]-U
gives the forward difference of the variable U along the L axis.
Ch3 Sec2.4.11. @SBX:n—boxcar smoother
The transformation @SBX applies a boxcar window (running mean) to smooth the variable along the indicated axis. The width of the boxcar is the number of points given as an argument to the transformation. All points are weighted equally, regardless of the sizes of the grid boxes, making this transformation best suited to axes with equally spaced points. If the number of points specified is even, however, @SBX weights the end points of the boxcar smoother as ½.. See General Information (p 76) for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0 u[L=1:120@SBX:5]
The transformation @SBX does not reduce the number of points along the axis; it replaces each of the original values with the average of its surrounding points. Regridding can be used to reduce the number of points.
Ch3 Sec2.4.12. @SBN:n—binomial smoother
The transformation @SBN applies a binomial window to smooth the variable along the indicated axis. The width of the smoother is the number of points given as an argument to the transformation. The weights are applied without regard to the widths of the grid boxes, making this transformation best suited to axes with equally spaced points. See General Information (p 76) for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0/Z=0 u[L=1:120@SBN:15]
The transformation @SBN does not reduce the number of points along the axis; it replaces each of the original values with a weighted sum of its surrounding points. Regridding can be used to reduce the number of points. The argument specified with @SBN, the number of points in the smoothing window, must be an odd value; an even value would result in an effective shift of the data along its axis.
Ch3 Sec2.4.13. @SHN:n—Hanning smoother
Transformation @SHN applies a Hanning window to smooth the variable along the indicated axis (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986). In other respects it is identical in function to the @SBN transformation. Note that the Hanning window used by Ferret contains only non-zero weight values with the window width. Some interpretations of this window function include zero weights at the end points. Use an argument of N-2 to achieve this effect (e.g., @SBX:5 is equivalent to a 7-point Hanning window which has zeros as its first and last weights). See General Information (p 76) for important details about this transformation.
Ch3 Sec2.4.14. @SPZ:n—Parzen smoother
Transformation @SPZ applies a Parzen window to smooth the variable along the indicated axis (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986). In other respects it is identical in function to the @SBN transformation. See General Information (p 76) for important details about this transformation.
Ch3 Sec2.4.15. @SWL:n—Welch smoother
Transformation @SWL applies a Welch window to smooth the variable along the indicated axis (ref. Numerical Recipes, The Art of Scientific Computing, by William H. Press et al., 1986). In other respects it is identical in function to the @SBN transformation. See General Information (p 76) for important details about this transformation.
Ch3 Sec2.4.16. @DDC—centered derivative
The transformation @DDC computes the derivative with respect to the indicated axis using a centered differencing scheme. The units of the underlying axis are treated as they are with integrations. If the points of the axis are unequally spaced, note that the calculation used is still (Fi+1 – Fi–1) / (Xi+1 – Xi–1) . See General Information (p 76) for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0/Z=0 u[L=1:120@DDC]
Ch3 Sec2.4.17. @DDF—forward derivative
The transformation @DDF computes the derivative with respect to the indicated axis. A forward differencing scheme is used. The units of the underlying axis are treated as they are with integrations. See General Information (p 76) for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0/Z=0 u[L=1:120@DDF]
Ch3 Sec2.4.18. @DDB—backward derivative
The transformation @DDF computes the derivative with respect to the indicated axis. A backward differencing scheme is used. The units of the underlying axis are treated as they are with integrations. See General Information (p 76) for important details about this transformation.
Example:
yes? PLOT/X=160W/Y=0/Z=0 u[L=1:120@DDB]
Ch3 Sec2.4.19. @NGD—number of good points
The transformation @NGD computes the number of good (valid) points of the variable with respect to the indicated axis. Use @NGD in combination with @SUM to determine the number of good points in a multi-dimensional region.
Note that, as with @VAR, when @NGD is applied simultaneously to multiple axes the calculation is applied to the entire block of values rather than to the individual axes. See General Information (p 76) for important details about this transformation.
Ch3 Sec2.4.20. @NBD—number of bad points
The transformation @NBD computes the number of bad (invalid) points of the variable with respect to the indicated axis. Use @NBD in combination with @SUM to determine the number of bad points in a multi-dimensional region.
Note that, as with @VAR, when @NBD is applied simultaneously to multiple axes the calculation is applied to the entire block of values rather than to the individual axes. See General Information (p 76) for important details about this transformation.
Ch3 Sec2.4.21. @SUM—unweighted sum
The transformation @SUM computes the unweighted sum (arithmetic sum) of the variable with respect to the indicated axis. This transformation is most appropriate for regions specified by subscript. If the region is specified in world coordinates, the edge points are not weighted—they are wholly included in or excluded from the calculation, depending on the location of the grid points with respect to the specified limits. See General Information (p 76) for important details about this transformation.
Ch3 Sec2.4.22. @RSUM—running unweighted sum
The transformation @RSUM computes the running unweighted sum of the variable with respect to the indicated axis. @RSUM is to @IIN as @SUM is to @DIN. The treatment of edge points is identical to @SUM. See General Information (p 76) for important details about this transformation.
Ch3 Sec2.4.23. @FAV:n—averaging filler
The transformation @FAV fills holes (values flagged as invalid) in variables with the average value of the surrounding grid points along the indicated axis. The width of the averaging window is the number of points given as an argument to the transformation. All of the surrounding points are weighted equally, regardless of the sizes of the grid boxes, making this transformation best suited to axes with equally spaced points. If the number of points specified is even, however, @FAV weights the end points of the filling region by 1/2. If any of the surrounding points are invalid they are omitted from the calculation. If all of the surrounding points are invalid the hole is not filled. See General Information (p 76) for important details about this transformation.
Example:
yes? CONTOUR/X=160W:160E/Y=5S:0 u[X=@FAV:5]
Ch3 Sec2.4.24. @FLN:n—linear interpolation filler
The transformation @FLN:n fills holes in variables with a linear interpolation from the nearest non-missing surrounding point. n specifies the number of points beyond the edge of the indicated axis limits to include in the search for interpolants (default n = 1). Unlike @FAV, @FLN is sensitive to unevenly spaced points and computes its linear interpolation based on the world coordinate locations of grid points.
Any gap of missing values that has a valid data point on each end will be filled, regardless of the length of the gap. However, when a sub-region from the full span of the data is requested sometimes a fillable gap crosses the border of the requested region. In this case the valid data point from which interpolation should be computed is not available. The parameter n tells Ferret how far beyond the border of the requested region to look for a valid data point. See General Information (p 76) for important details about this transformation.
Example: To allow data to be filled only when gaps in i are less than 15 points, use the @CIA and @CIB transformations which return the distance from the nearest valid point.
yes? USE my_data
yes? LET allowed_gap = 15
yes? LET gap_size = my_var[i=@cia]
+ my_var[i=@cib]
yes? LET gap_mask = IF gap_size LE gap_allowed THEN 1
yes?
LET my_answer = my_var[i=@fln) * gap_mask
Ch3 Sec2.4.25. @FNR:n—nearest neighbor filler
The transformation @FNR:n is similar to @FLN:n, except that it replicates the nearest point to the missing value. In the case of points being equally spaced around the missing point, the mean value is used. See General Information (p 76) for important details about this transformation.
Ch3 Sec2.4.26. @LOC—location of
The transformation @LOC accepts an argument value—the default value is zero if no argument is specified. The transformation @LOC finds the single location at which the variable first assumes the value of the argument. The result is in units of the underlying axis. Linear interpolation is used to compute locations between grid points. If the variable does not assume the value of the argument within the specified region the @LOC transformation returns an invalid data flag.
For example, temp[Z=0:200@LOC:18] finds the location along the Z axis (often depth in meters) at which the variable "temp" (often temperature) first assumes the value 18, starting at Z=0 and searching to Z=200. See General Information (p 76) for important details about this transformation.
yes? CONTOUR/X=160E:160W/Y=10S:10N temp[Z=0:200@LOC:18]
produces a map of the depth of the 18-degree isotherm. See also the General Information about transformations section in this chapter (p. 76).
Note that the transformation @LOC can be used to locate non-constant values, too, as the following example illustrates:
Example: locating non-constant values
Determine the depth of maximum salinity.
yes? LET max_salt = salt[Z=@MAX]
yes? LET zero_at_max = salt - max_salt
yes?
LET depth_of_max = zero_at_max[Z=@LOC:0]
Ch3 Sec2.4.27. @WEQ—weighted equal; integration kernel
The @WEQ ("weighted equal") transformation is the subtlest and arguably the most powerful transformation within Ferret. It is a generalized version of @LOC; @LOC always determines the value of the axis coordinate (the variable X, Y, Z, or T) at the points where the gridded field has a particular value. More generally, @WEQ can be used to determine the value of any variable at those points. See General Information (p 76) for important details about this transformation.
Like @LOC, the transformation @WEQ finds the location along a given axis at which the variable is equal to the given (or default) argument. For example, V1[Z=@WEQ:5] finds the Z locations at which V1 equals "5". But whereas @LOC returns a single value (the linearly interpolated axis coordinate values at the locations of equality) @WEQ returns instead a field of the same size as the original variable. For those two grid points that immediately bracket the location of the argument, @WEQ returns interpolation coefficients. For all other points it returns missing value flags. If the value is found to lie identically on top of a grid point an interpolation coefficient of 1 is returned for that point alone. The default argument value is 0.0 if no argument is specified.
Example 1
yes? LET v1 = X/4
yes? LIST/X=1:6 v1, v1[X=@WEQ:1], v1[X=@WEQ:1.2]
X
v1 @WEQ:1 @WEQ:1.2
___ _____ ______ ________
1: 0.250 .... ....
2: 0.500 .... ....
3: 0.750 ....
....
4: 1.000 1.000 0.2000
5: 1.250 .... 0.8000
6: 1.500
.... ....
The resulting field can be used as an "integrating kernel," a weighting function that when multiplied by another field and integrated will give the value of that new field at the desired location.
Example 2
Using variable v1 from the previous example, suppose we wish to know the value of the function X^2 (X squared) at the location where variable v1 has the value 1.2. We can determine it as follows:
yes? LET x_squared = X^2
yes? LET integrand = x_squared * v1[X=@WEQ:1.2]
yes?
LIST/X=1:6 integrand[X=@SUM] !Ferret output below
X_SQUARED *
V1[X=@WEQ:1.2]
X: 1 to 6 (summed)
23.20
Notice that 23.20 = 0.8 * (5^2) + 0.2 * (4^2)
Below are two "real world" examples that produce fully labeled plots.
Example 3: salinity on an isotherm
Use the Levitus climatology to contour the salinity of the Pacific Ocean along the 20-degree isotherm (Figure 3_5).
yes? SET DATA levitus_climatology ! annual sub-surface climatology
Example 4: month with warmest sea surface temperatures
Use the COADS data set to determine the month in which the SST is warmest across the Pacific Ocean. In this example we use the same principles as above to create an integrating kernel on the time axis. Using this kernel we determine the value of the time step index (which is also the month number, 1–12) at the time of maximum SST (Figure 3_6).
yes? SET DATA coads_climatology ! monthly surface climatology
yes?
SET REGION/X=100E:50W/Y=45S:45N ! Pacific Ocean
yes? SET MODE CAL:MONTH
yes?
LET zero_at_warmest = sst - sst[l=@max]
yes? LET integrand = L[G=sst] *
zero_at_warmest[L=@WEQ] ! "L" is 1 to 12
yes? SET VARIABLE/TITLE="Month
of warmest SST" integrand
yes? SHADE/L=1:12/PAL=inverse_grayscale integrand[L=@SUM]
Ch3 Sec2.4.28. @ITP—interpolate
The @ITP transformation provides the same linear interpolation calculation that is turned on modally with SET MODE INTERPOLATE but with a higher level of control, as @ITP can be applied selectively to each axis. @ITP may be applied only to point locations along an axis. The result is the linear interpolation based on the adjoining values. See General Information (p 76) for important details about this transformation.
For example, for a Z axis with points at Z=0, 10, 20, ...
V[Z=4@ITP] will compute 0.6 * V[Z=0] + 0.4 * V[Z=10]
Ch3 Sec2.4.29. @CDA—closest distance above
The transformation @CDA will compute at each grid point how far it is to the closest valid point above this coordinate position on the indicated axis. The distance will be reported in the units of the axis. If a given grid point is valid (not missing) then the result of @CDA for that point will be 0.0. See the example for @CDB below. The result's units are now axis units, e.g., degrees of longitude to the next valid point above. See General Information (p 76) for important details about this transformation, and see the example under @CDB below (p 91).
Ch3 Sec2.4.30. @CDB—closest distance below
The transformation @CDB will compute at each grid point how far it is to
the closest valid point below this coordinate position on the indicated
axis. The distance will be reported in the units of the axis. If a given
grid point is valid (not missing) then the result of @CDB for that point
will be 0.0. The result's units are now axis units, e.g., degrees of longitude
to the next valid point below. See General Information (p 76) for important
details about this transformation.
Example:
yes? USE coads_climatology
Ch3 Sec2.4.31.
@CIA—closest index above
The transformation @CIA will compute at each grid point how far it is to
the closest valid point above this coordinate position on the indicated
axis. The distance will be reported in terms of the number of points (distance
in index space). If a given grid point is valid (not missing) then the
result of @CIA for that point will be 0.0. See the example for @CIB below.
The units of the result are grid indices; integer number of grid units
to the next valid point above. See General Information (p 76) for important
details about this transformation, and see the example under @CIB below
(p 92).
Ch3 Sec2.4.32.
@CIB—closest index below
The transformation @CIB will compute at each grid point how far it is to
the closest valid point below this coordinate position on the indicated
axis. The distance will be reported in terms of the number of points (distance
in index space). If a given grid point is valid (not missing) then the
result of @CIB for that point will be 0.0. The units of the result are
grid indices, integer number of grid units to the next valid point below.
See General Information (p 76) for important details about this transformation.
Example:
yes? USE coads_climatology
Ch3 Sec2.5.
IF-THEN logic ("masking")
Ferret expressions can contain embedded IF-THEN-ELSE logic. The syntax
of the IF-THEN logic is simply (by example)
LET a = IF a1 GT b THEN a1 ELSE a2
(read as "if a1 is greater than b then a1 else a2").
This syntax is especially useful in creating masks that can be used to
perform calculations over regions of arbitrary shape. For example, we can
compute the average air-sea temperature difference in regions of high wind
speed using this logic:
SET DATA coads_climatology
The user may find it clearer to think of this logic as WHERE-THEN-ELSE
to aviod confusion with the IF used to control conditional execution of
commands. Compound and multi-line IF-THEN-ELSE constructs are not allowed
in embedded logic.
Ch3 Sec2.6.
Lists of constants ("constant arrays")
The syntax {val1, val2, val3} is a quick way to enter a list of constants.
For example
yes? LIST {1,3,5}, {1,,5}
Note that a constant variable is always an array oriented in the X direction
To create a constant aray oriented in, say, the Y direction use YSEQUENCE
yes? STAT/BRIEF YSEQUENCE({1,3,5})
Below are two examples illustrating uses of constant arrays. (See the
constant_array_demo journal file)
Ex. 1) plot a triangle (Figure 3_7)
Or multiple triangles (Figure 3_8) See polymark.jnl regarding this figure
yes? SET REGION/x=125w:109w/y=55s/l=1
yes? LIST
sst, sst[x=@cda], sst[x=@cdb] ! results below
Column 1: SST is SEA SURFACE
TEMPERATURE (Deg C)
Column 2: SST[X=@CDA:1] is SEA SURFACE TEMPERATURE
(Deg C) (closest dist above on X ...)
Column 3: SST[X=@CDB:1] is SEA SURFACE
TEMPERATURE (Deg C) (closest dist below on X ...)
SST
SST SST
125W / 108: 6.700 0.000 0.000
123W / 109: ....
8.000 2.000
121W / 110: .... 6.000 4.000
119W / 111: ....
4.000 6.000
117W / 112: .... 2.000 8.000
115W / 113: 7.800
0.000 0.000
113W / 114: 7.800 0.000 0.000
111W / 115: ....
2.000 2.000
109W / 116: 8.300 0.000 0.000
yes? SET REGION/x=125w:109w/y=55s/l=1
yes? LIST
sst, sst[x=@cia], sst[x=@cib] ! results below
Column 1: SST is SEA SURFACE
TEMPERATURE (Deg C)
Column 2: SST[X=@CIA:1] is SEA SURFACE TEMPERATURE
(Deg C) (closest dist above on X ...)
Column 3: SST[X=@CIB:1] is SEA SURFACE
TEMPERATURE (Deg C) (closest dist below on X ...)
SST
SST SST
125W / 108: 6.700 0.000 0.000
123W / 109: ....
4.000 1.000
121W / 110: .... 3.000 2.000
119W / 111: ....
2.000 3.000
117W / 112: .... 1.000 4.000
115W / 113: 7.800
0.000 0.000
113W / 114: 7.800 0.000 0.000
111W / 115: ....
1.000 1.000
109W / 116: 8.300 0.000 0.000
SET REGION/X=100W:0/Y=0:80N/T=15-JAN
LET fast_wind
= IF wspd GT 10 THEN 1
LET tdiff = airt - sst
LET fast_tdiff = tdiff * fast_wind
X: 0.5 to 3.5
Column 1: {1,3,5}
Column 2:
{1,,5}
{1,3,5} {1,,5}
1 / 1: 1.000 1.000
2 / 2: 3.000
....
3 / 3: 5.000 5.000
Total # of data points: 3 (1*3*1*1)
# flagged as bad data: 0
Minimum value: 1
Maximum value: 5
Mean
value: 3 (unweighted average)
LET xtriangle = {0,.5,1}
LET ytriangle = {0,1,0}
POLYGON/LINE=8 xtriangle,
ytriangle, 0
Ex. 2) Sample Jan, June, and December from sst in coads_climatology
USE coads_climatology
LET my_sst_months = SAMPLEL({1,6,12}, sst)
STAT/BRIEF my_sst_months
yes? STAT/BRIEF my_sst_months
Total # of data points: 48600 (180*90*1*3)
# flagged as bad data: 21831
Minimum value: -2.6
Maximum value: 31.637
Mean value: 17.571 (unweighted average)
Ch3 Sec3. EMBEDDED EXPRESSIONS
Ferret supports "immediate mode" mathematical expressions—that is, numerical expressions that may be embedded anywhere within a command line. These expressions are evaluated immediately by Ferret—before the command itself is parsed and executed. Immediate mode expressions are enclosed in grave accents, the same syntax used by the Unix C shell. Prior to parsing and executing the command Ferret will replace the full grave accent expression, including the accent marks, with an ASCII string representing the numerical value. For example, if the given command is
CONTOUR/Z=`temp[X=180,Y=0,Z=@LOC:15]` salt
Ferret will evaluate the expression "temp[X=180,Y=0,Z=@LOC:15]" (the depth of the 15-degree isotherm at the equator/dateline—say, it is 234.5 meters). Ferret will generate and execute the command
CONTOUR/Z=234.5 salt
Embedded expressions:
Embedded expressions: the expression must evaluate to a single number, a scalar, or Ferret will respond that the command contains an error if the result is invalid the numerical string will be "bad" (see BAD= in following section, p. 97). Region qualifiers that begin a command containing an embedded expression will be used in the evaluation of the expression. If multiple embedded expressions are used in a single command they will be evaluated from left to right within the command. This means that embedded expressions used to specify region information (e.g., the above example) may influence the evaluation of other embedded expressions to the right. When embedded expressions are used within commands that are arguments of a REPEAT command their evaluation is deferred until the commands are actually executed. Thus the embedded expressions are re-evaluated at each loop index of the REPEAT command. Grave accents have a higher priority than any other syntax character. Thus grave accent expressions will be evaluated even if they are enclosed within quotation marks, parentheses, square brackets, etc. Substitutions based on dollar-signs (command script arguments and symbols) will be made before embedded expressions are evaluated. A double grave accent will be translated to a single grave accent and not actually evaluated. Thus double grave accents provide a mechanism to defer evaluation so that grave accent expressions may be passed to the Unix command line with the SPAWN command or may be passed as arguments to GO scripts (to be evaluated INSIDE the script). The state of MODE VERIFY will determine if the evaluation of the embedded expression is echoed at the command line—similar to REPEAT loops.
Ch3 Sec3.1. Special calculations using embedded expressions
By default Ferret formats the results of embedded expressions using 5 significant digits. If the result of the expression is invalid (e.g., 1/0) the result by default is the string "bad". Controls allow you to specify the formatting of embedded expression results in both valid and invalid cases and to query the size and shape of the result.
The syntax to achieve this control is KEYWORD=VALUE pairs inside the grave accents, following the expression and set off by commas. The recognized keywords are "BAD=", "PRECISION=", and "RETURN=". Only the first character of the keyword is significant, so they may be abbreviated as "B=", "P=", and "R=".
PRECISION=, BAD=, and RETURN= may be specified simultaneously, in any order, separated by commas. If RETURN= is included, however, the other keywords will be ignored.
can be used to control the number of significant digits displayed, up to a maximum of 10 (actually at most 7 digits are significant since Ferret calculations are performed in single precision). Ferret will, however, truncate terminating zeros following the decimal place. Thus
SAY `3/10,PRECISION=7`
will result in
0.3
instead of 0.3000000.
If the value specified for #digits is negative Ferret will interpret this as the desired number of decimal places rather than the number of significant digits. Thus
SAY `35501/100,P=-2`
will result in
355.01
instead of 355.
In the case of a negative precision value, Ferret will again drop terminating
zeros to the right of the decimal point.
can be used to control the text which is produced when the result of the
immediate mode expression is invalid. Thus
SAY `1/0,BAD=missing`
will result in
missing
or
SAY `1/0,B=-999`
will result in
-999
The keyword RETURN= can reveal the size and shape of the result. RETURN=
may take arguments
The RETURN= option in immediate mode expressions does not actually compute
the result unless it must. For example, the expression
`sst, RETURN=TEND`
will return the formatted coordinate for the last point on the T axis of
variable sst without actually reading or computing the values of sst. This
allows Ferret scripts to be constructed so that they can anticipate the
size of variables and act accordingly.
Note that this does not apply to variable definitions which involve grid-changing
variables that return results on ABSTRACT axes. For those variables the
size and shape of the result may depend on data values, so the entire result
must be computed in order to determine many of the return= attributes
returns the 4-dimensional shape of the result—i.e., a list of those axes
along which the result comprises more than a single point. For example,
a global sea surface temperature field at a single point in time:
SAY `SST[T=1-JAN-1983],RETURN=SHAPE`
will result in
XY
See Symbol Substitutions in the chapter "Handling String Data" (p. 170) for
examples showing the special utility of this feature.
RETURN=ISTART (and similarly JSTART, KSTART, and LSTART)
returns the starting index of the result along the indicated axis: I, J,
K, or L. For example, if CAST is a vertical profile with points every 10
meters of depth starting at 10 meters then Z=100 is the 10th vertical point,
so
SAY `CAST[Z=100:200],RETURN=KSTART`
will result in
10
RETURN=IEND (and similarly JEND, KEND, and LEND)
returns the ending index of the result along the indicated axis: I, J,
K, or L. In the example above
SAY `CAST[Z=100:200],RETURN=KEND`
will result in
20
The size and shape information revealed by RESULT= is useful in creating
sophisticated scripts. For example, these lines could be used to verify
that the user has passed a 1-dimensional field as the first argument to
a script
LET my_expr = $1
RETURN=XSTART (and similarly YSTART, ZSTART, and TSTART)
returns start of specified world coordinate region
RETURN=XEND (and similarly YEND, ZEND, and TEND)
returns end of specified world coordinate region
return the total number of points in the variable -- Nx*Ny*Nz*Nt
returns the T0 string from the time axis
returns the units string from the variable
returns the title of a variable
returns the grid name of a variable
RETURN=IAXIS (and similarly JAXIS, KAXIS, and LAXIS)
Returns the name of an axis on which the variable is defined.
RETURN=XAXIS (and similarly YAXIS, ZAXIS, and TAXIS)
Returns the name of an axis on which the variable is defined.
Ch3 Sec4.
DEFINING NEW VARIABLES
The ability to define new variables lies at the heart of the computational
power that Ferret provides. Complex analyses in Ferret generally proceed
as hierarchies of simple variable definitions. As a simple example, suppose
we wish to calculate the root mean squared value of variable, V, over 100
time steps. We could achieve this with the simple hierarchy of definitions:
LET v_rms = v_mean_sq ^ 0.5
As the example shows, the variables can be defined in any order and without
knowledge in advance of the domain over which they will be evaluated. As
variable definitions are given to Ferret with the LET (alias for DEFINE
VARIABLE) command the expressions are parsed but not evaluated. Evaluation
occurs only when an actual request for data is made. In the preceding example
this is the point at which the LIST command is given. At that point Ferret
uses the current context (SET REGION and SET DATA_SET) and the command
qualifiers (e.g., "L=1:100") to determine the domain for evaluation. Ferret
achieves great efficiency by evaluating only the minimum subset of data
required to satisfy the request.
One consequence of this approach is that definitions such as
LET a = a + 1 ! nonsense
are nonsense within Ferret. The value(s) of variable "a" come into existence
only as they are called for, thus it is nonsense for them to appear simultaneously
on the left and right of an equal sign.
Variable names can be 1 to 24 characters in length and begin with a letter.
See the command reference DEFINE VARIABLE (p. 262) for the available qualifiers.
Ch3 Sec4.1.
Global, local, and default variable definitions
All of the above definitions are examples of "global variable definitions."
A global variable definition applies to all data sets. In the above example
the expression "v_rms[D=dset_1]" would be based on the values and domain
of the variable V from data set dset_1 and "v_rms[D=dset_2]" would similarly
be drawn from data set dset_2. The domain of v_rms, its size, shape, and
resolution, will depend on the particular data set in which it is evaluated.
Although global variables are simple to use they can lead to ambiguities.
Suppose, for example, that data sets dset_1 and dset_2 contain the following
variables:
Dset_1 dset_2
If we would like to compare speeds from the two data sets we might be tempted
to define a new variable, speed, as
LET speed = (u*u + v*v)^0.5
In doing so, however, we create an ambiguity of interpretation for the
expression "speed[d=dset_1]".
To avoid this ambiguity we need to create a variable definition, "speed,"
that is local to data set dset_2. The qualifier /D= used as follows
LET/D=dset_2 speed = (u*u + v*v)^0.5 ! in dset_2, only
provides this capability. The use of /D=dset_2 indicates that this new
definition of "speed" applies only to data set dset_2.
A convenient shortcut is often to define a "default variable." A default
variable is defined using the /D qualifier with no argument
LET/D speed = (u*u + v*v)^0.5 ! where "speed" doesn't already exist
As a default variable "speed" is a definition that applies only to data
sets that would otherwise not posses a variable named speed. In this sense
it is a fallback default.
Ch3 Sec5.
DEBUGGING COMPLEX HIERARCHIES OF EXPRESSIONS
A complex analysis generally proceeds within Ferret as a complex hierarchy
of expressions: variables defined in terms of other variables defined in
terms of other variables, etc., often containing many levels of transformation.
When an error message such as "can only contour or vector a 2D region"
occurs it may appear difficult to locate the reason for this message.
A simple strategy to locate the source of such problems is to use the command
STAT which shows the size and shape of variables and expressions (simply
edit the offending command line, replacing the PLOT, CONTOUR, VECTOR, etc.
command with STAT and eliminating qualifiers if necessary) and use SHOW
VARIABLE to see the variable definitions. By repeatedly using STAT to examine
the component variables of definitions one can quickly locate the source
of the problem.
DEFINE SYMBOL SHAPE `my_expr,RESULT=SHAPE`
QUERY/IGNORE
($SHAPE%|X|Y|Z|T|<Expression must be 1-dimensional%)
LET v_mean_sq = v_squared[L=@AVE]
LET v_squared
= v * v
SET VARIABLE/TITLE="RMS V" v_rms
LIST/L=1:100 v_rms
(listed output
not included)
______ ______
speed u, v